Eindig of oneindig groot?
De Big Bang-theorie is sterk gebaseerd op de algemene relativiteitstheorie van Einstein, die het verband beschrijft tussen ruimte, tijd en zwaartekracht.
Waarnemingen tonen aan dat de massa in het heelal erg homogeen verdeeld is. Dit maakt het mogelijk om betrekkelijk eenvoudig het heelal te beschrijven met de formules uit de algemene relativiteitstheorie: globaal gezien is overal het effect van de zwaartekracht gelijk! Deze veronderstelling van uniformiteit van het heelal (homogeen en isotroop) is dan ook erg belangrijk voor de kosmologen, en wordt het kosmologisch principe genoemd.
De algemene relativiteitstheorie stelt dat de ruimte kromt onder invloed van aanwezige massa (de zwaartekracht). Geldt het effect van massa (de zwaartekracht) die de ruimte om zich heen "kromt", dan is rechtdoor niet meer gewoon rechtdoor. In de 3-dimensionale wereld die we kennen kunnen wij ons dit moeilijk voorstellen, maar gelukkig kunnen we ons beroepen op een 2-dimensionaal voorbeeld om hier meer gevoel voor te krijgen (zie kaderstuk).
Leven in een gekromde wereld
Neem een geruit laken en span het op. Het is nu mooi strak. Stel dat je een wezen bent dat in dit laken beweegt, en zich enkel bewust is van het laken zelf, en dus niet van de ruimte errond. De "ruimte" van dat wezen is dus 2-dimensionaal, in tegenstelling tot onze 3-dimensionale wereld. De twee hoofdrichtingen waarin het wezen zich kan bewegen, zijn de richtingen van de ruitjes op het laken. Als het wezen volgens deze lijnen beweegt, gaat het volgens zijn eigen waarneming "rechtdoor".

Stel nu dat we het laken vervormen, door er een gewicht op te leggen. Het laken is nu gekromd. Het wezen, dat volgens de ruitjes loopt, en volgens zijn eigen waarneming in de 2-dimensionale wereld dus rechtdoor, zal in de 3-dimensionale wereld een gekromd pad volgen.
Zo ook volgen wij in onze 3-dimensionale wereld, als we rechtdoor gaan in de nabijheid van massa, eigenlijk een gekromd pad in de 4-dimensionale tijd-ruimte wereld.
De kromming van het heelal
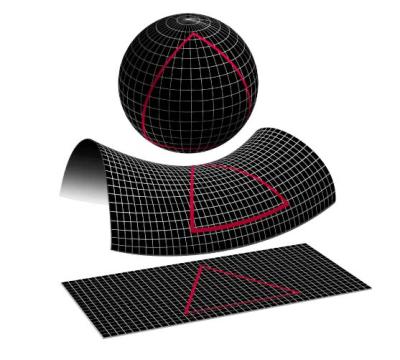
Aangezien de massa in het heelal, volgens het kosmologisch principe, globaal bekeken gelijkmatig verdeeld is, betekent dat ook dat het heelal overal even gekromd is, en dat we dus de kromming van het heelal voor het ganse heelal ineens kunnen gaan onderzoeken.
Naargelang de massa-dichtheid in het heelal, zijn er drie mogelijke situaties: de kromming van de ruimte kan positief zijn, negatief, of nul. Ook hier is het zich voorstellen in een 3-dimensionale ruimte moeilijk, maar kunnen we daarvoor teruggrijpen naar het 2-dimensionale analogon, zoals in de figuur hiernaast.
Als er geen kromming is, is de ruimte vlak, zoals wij hem ons spontaan voorstellen. In elke richting kan je dan oneindig ver doorlopen. Het volume van het heelal is dan oneindig. Deze situatie kan echter enkel als het heelal "toevallig" nét een welbepaalde massadichtheid heeft, die we de "kritische massadichtheid" noemen. Men weet dat de kritische dichtheid erg laag is, zowat het gewicht van 6 waterstofatomen per kubieke meter.
Bij positieve kromming zien we dat de ruimte een eindig volume heeft (de bol uit ons analogon heeft een eindige oppervlakte), en dat je, als je maar lang genoeg rechtdoor gaat, terug op dezelfde plek uitkomt. Dit kan enkel als de dichtheid van het heelal groter is dan de kritische massadichtheid.
Bij negatieve kromming is het volume van het heelal terug oneindig. De massadichtheid moet dan lager zijn dan de kritische massadichtheid. In twee dimensies heeft een oppervlak met negatieve kromming een zadelvorm.
Evolutie in de tijd
Een andere vraag is hoe het heelal nu verder zal evolueren. De uitdijing van het heelal wordt tegengewerkt door de zwaartekracht, die juist probeert alle hemellichamen bij elkaar te houden. Al naargelang de hoeveelheid materie aanwezig in het heelal doen zich de drie zelfde gevallen als hierboven voor.
Een eerste mogelijkheid, als we te maken hebben met een heelal met positieve kromming, is dat ooit de uitzetting van het heelal door de zwaartekracht tot stilstand zal komen en overgaan in een ineenkrimping, tot er een omgekeerde Big Bang komt, een big crunch. In dat geval spreekt men van een gesloten heelal. Dit wordt geïllustreerd door de gele lijn op de grafiek hieronder.
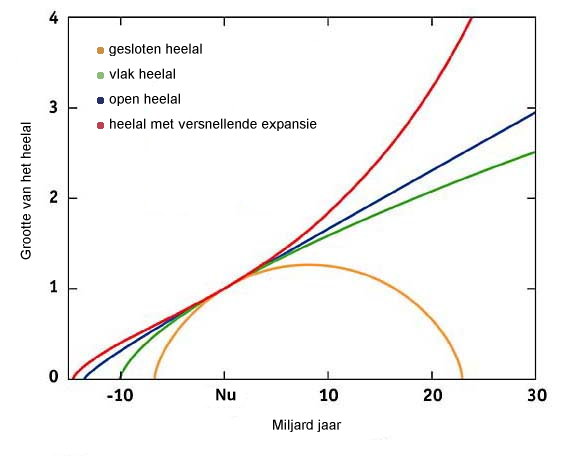
Als de kromming negatief is (blauwe lijn), zitten we in een open heelal. De uitdijing wordt door de zwaartekracht wel vertraagd, maar zal nooit stoppen. Een "vlak" heelal (groene lijn), is het grensgeval tussen de twee vorige. Het heelal blijft uitdijen, maar de expansiesnelheid wordt op den duur willekeurig klein.
Mogelijk is daarmee nog niet alles gezegd. In 1999 onderzochten astronomen hoeveel de constante van Hubble bedraagt in verafgelegen melkwegstelsels, om zo te weten te komen hoe de uitdijingssnelheid van het heelal afneemt met de tijd. Deze metingen hebben echter aangetoond dat de uitdijingssnelheid niet afneemt, maar toeneemt! Erg recent (2002) werd dit via een andere meettechniek bevestigd. Indien dit het geval is, moeten we terugvallen op de rode curve, dat van een heelal met een toenemende expansiesnelheid. Deze keuze laat verder nog toe dat het heelal vlak, positief of negatief gekromd is.
Is het heelal nu open of gesloten? Eindig of oneindig?
Uit bovenstaande blijkt dat we dus de massa-dichtheid van het heelal moeten achterhalen, en dit vergelijken met de kritische dichtheid, die om en bij de 10-26 kg/m3 bedraagt.
Als we in het heelal rondkijken en het gewicht schatten van al wat we zien, komen we nog maar op ca. 1% uit van de kritische massa. Zelfs als we rekening houden met het stof dat we niet kunnen zien maar dat wel het licht van verderaf gelegen sterren tegenhoudt of verzwakt, komen we hooguit aan 5%. Moeten we hieruit besluiten dat de dichtheid van het heelal onder de kritische massadichtheid ligt, en dat we daarom in een open universum leven? Nog niet.
Donkere materie
Kosmologen vermoeden dat er in het heelal een grote hoeveelheid "donkere materie" is. Deze materie wordt donker genoemd, omdat men ze via elektromagnetische golven (licht, radiostraling, ...) niet kan waarnemen. In tegenstelling tot klassiek stof, verzwakt donkere materie het licht van verderaf gelegen sterren niet. De gravitationele effecten van donkere materie zijn echter wel waarneembaar.
Zo merkt men dat melkwegstelsels niet draaien zoals zij zouden moeten draaien indien ze enkel de zichtbare massa zouden bevatten. Ook ten opzichte van mekaar bewegen melkwegstelsels niet als verwacht. Als men veronderstelt dat sterrenstelsels omgeven worden door een halo van donkere materie, kan men deze bewegingen wel verklaren.
Men heeft verschillende aanwijzingen dat de donkere materie niet uit gewone atomen of atoomkernen bestaat. Waaruit ze dan wel bestaat, is nog een raadsel. Het zouden een andere soort elementaire deeltjes kunnen zijn (neutrino's, nog niet ontdekte deeltjes, ...), of bijzondere objecten (zwarte gaten, MACHO's, ...).
Er zijn aanwijzingen dat er in ons heelal een grote hoeveelheid donkere materie aanwezig is (zie kaderstuk). Gewone en donkere materie samen zouden 30% van de kritische massa kunnen leveren.
Misschien is het ook niet nodig om de volledige kritische massa te verzamelen. De recente waarnemingen, die erop zouden wijzen dat we in een heelal met versnellende uitdijing leven, suggereren het bestaan van een "kosmologische constante", die een deel van de vereiste massa zou compenseren... Men spreekt in dit verband soms ook over "donkere energie". Deze donkere energie zou de gravitatiekrachten, die de uitzetting proberen af te remmen, tegenwerken. Donkere energie zou de ontbrekende 70% van de kritische dichtheid kunnen leveren. Er bestaan theorieen over de aard van donkere materie, die met behulp van de Large Hadron Collider (LHC) hopelijk experimenteel zullen kunnen worden getoetst. Over de aard van donkere energie, daarentegen, tast men momenteel nog - letterlijk en figuurlijk - volledig in het duister.
Conclusie
De beste waarnemingen tot hiertoe wijzen uit dat het heelal vlak is, zij het dat 68% van de kritische dichtheid vertegenwoordigd wordt door donkere energie die ervoor zorgt dat de expansie na een aanvankelijke vertraging door de zwaartekracht terug wordt versneld.
Van de overige 32% is het overgrote deel donkere materie. Slechts ongeveer 5% van de kritische dichtheid wordt ingenomen door klassieke materie en energie, zoals wij die kennen. Maar ongeveer 1% van de kritische dichtheid bestaat uit sterren.
Alhoewel het hierboven geschetste beeld bevestigd wordt door de waarnemingen, blijven kosmologen toch met een reuzengroot ei zitten, omdat zij 95% van de inhoud van het heelal niet bevredigend kunnen beschrijven. Zo lang moeten we in onze conclusies hierboven toch nog een slag om de arm houden.
Of het heelal eindig of oneindig is, wij kunnen er alleszins maar een beperkt deel van zien en ervaren. Als het hierboven geschetste beeld correct is, heeft de "big bang" 13,8 miljard jaar geleden plaats gevonden. Alleen objecten waarvan het licht en de straling ons in die tijdsspanne heeft kunnen bereiken, behoren tot het waarneembare heelal. Wat zich daarbuiten afspeelt kan men niet meten, maar het kosmologisch principe doet ons vermoeden dat het daar net is zoals hier.
 Volkssterrenwacht Urania
Volkssterrenwacht Urania